【331838】第二章 二次函数周周测4（2.2）

2.2 二次函数的图像与性质

一、 选择题

1. 抛物线 y ＝( x －2) ² +3的顶点坐标是（　　）．

A．(2,3)   B．(－2,3)     C．(2，－3)   D．(－2，－3)

2. 把抛物线 y ＝－ x ² 向右平移1个单位，然后向下平移3个单位，则平移后抛物线的表达式为（　　）．

A． y ＝－( x －1) ² +3   B． y ＝－( x +1) ² +3   C． y ＝－( x －1) ² －3   D． y ＝－( x +1) ² －3

3. 已知二次函数 y ＝－ x ² + bx + c 中函数 y 与自变量 x 之间的部分对应值如下表所示，点 A ( x ₁ ， y ₁ )， B ( x ₂ ， y ₂ )在函数的图象上，当0＜ x ₁ ＜1，2＜ x ₂ ＜3时， y ₁ 与 y ₂ 的大小关系正确的是（　　）．

A． y ₁ ≥ y ₂   B． y ₁ ＞ y ₂    C． y ₁ ＜ y ₂   D． y ₁ ≤ y ₂

4. 若把函数 y ＝ x 的图象用 E ( x ， x )表示，函数 y ＝2 x +1的图象用 E ( x, 2 x +1)表示，…，则 E ( x ， x ² －2 x +1)可以由 E ( x ， x ² )怎样平移得到（　　）．

A．向上平移1个单位     B．向下平移1个单位

C．向左平移1个单位     D．向右平移1个单位

5. 下列抛物线中，开口最大的是（　　）

A．   B． C． y ＝－ x ²        D．

6. 抛物线 的顶点坐标和对称轴分别是（　　）

A．(1，2)，直线 x ＝1

B．(－1，2)，直线 x ＝－1

C．(－4，－5)，直线 x ＝－4

D．(4，－5)，直线 x ＝4

7. 二次函数 y ＝ x ² 的图象向右平移3个单位，得到新的图象的函数关系式是（　　）

A． y ＝ x ² +3 B． y ＝ x ² －3

C． y ＝( x +3) ²   D． y ＝( x －3) ²

8. 已知函数 y ＝－3 x ² +1的图象是抛物线，若该抛物线不动，把 x 轴向上平移两个单位， y 轴向左平移一个单位，则该函数在新的直角坐标系内的函数关系式为（　　）

A． y ＝－3( x +1) ² +2   B． y ＝－3( x －1) ² －1

C． y ＝3( x +1) ² +2    D． y ＝3( x －1) ² －2

9. 在平面直角坐标系中，函数 y ＝－ x +1与 y ＝ ( x －1) ² 的图象大致是（　　）

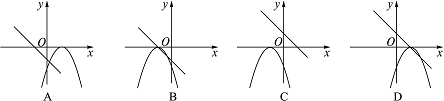
10. 二次函数 y ＝ ax ² + bx + c 中， b ² ＝ ac ，且 x ＝0时， y ＝－4，则（　　）

A． y _最大值 ＝－4 B． y _最小值 ＝－4

C． y _最大值 ＝－3 D． y _最小值 ＝－3

二、填空题

11. 将 y ＝2 x ² －12 x －12变为 y ＝ a ( x － m ) ² + n 的形式，则 m n ＝__________.

12. 当 x ＝__________时，二次函数 y ＝ x ² +2 x －2有最小值．

13. 抛物线 y ＝2 x ² － bx +3的对称轴是直线 x ＝1，则 b 的值为__________．

14. 已知抛物线 y ＝ ax ² + bx + c ( a ＞0)的对称轴为直线 x ＝1，且经过点(－1， y ₁ )，(2， y ₂ )，试比较 y ₁ 和 y ₂ 的大小： y ₁ __________ y ₂ (填“＞”“＜”或“＝”)．

15. 二次函数的一般式为____________；若抛物线的顶点坐标为（h，k），则可设该抛物线的顶点式为____________；若抛物线与x轴交于（x ₁ ，0）、（x ₂ ，0），则可设该抛物线的两点式为____________.

16. 抛物线y=ax ² +bx+c的形状与y=2x ² -4x-1相同，对称轴平行于y轴，且x=2时，y有最大值-5，该抛物线关系式为____________.

三、解答题

17. 已知反比例函数 的图象经过点(－1,－2).

（1）求 y 与 x 的函数关系式;

（2）若点(2, n )在这个图象上,求 n 的值.

18.如图所示的二次函数 的图象中，刘星同学观察得出了下面四条信息：（1） ；（2）c>1；（3）2a－b<0；（4）a+b+c<0。你认为其中错误的有（　　）

A．2个 B．3个 C．4个 D．1个

19.如图，已知A（a，m）、B（2a，n）是反比例函数y= （k＞0）与一次函数y=- x+b图象上的两个不同的交点，分别过A、B两点作x轴的垂线，垂足分别为C、D，连结OA、OB，若已知1≤a≤2，则求S _△OAB 的取值范围．

20.已知反比例函数 和一次函数y=-x+a-1（a为常数）
（1）当a＝5时，求反比例函数与一次函数的交点坐标（5分）
（2）是否存在实数a，使反比例函数与一次函数有且只有一个交点，如果存在，求出实数a，如果不存在，说明理由（5分）

答案解析部分(共有 20 道题的解析及答案)

一、选择题

1、A

点拨： 二次函数 y ＝ a ( x － h ) ² + k ( a ≠0)的顶点坐标是( h ， k )．

2、C

点拨： 抛物线 y ＝－ x ² 向右平移1个单位，得到 y ＝－( x －1) ² ，再下平移3个单位，得到 y ＝－( x －1) ² －3.

3、C

点拨： 由题中条件可知，该抛物线的对称轴是 x ＝2，且开口向下，∴当0＜ x ₁ ＜1,2＜ x ₂ ＜3时， y ₁ ＜ y ₂ .

4、D

点拨： 根据给出的新定义， E ( x ， x ² －2 x +1)为函数 y ＝ x ² －2 x +1的图象， E ( x ， x ² )为函数 y ＝ x ² 的图象．因为 y ＝ x ² －2 x +1＝( x －1) ² ，因此只要把函数 y ＝ x ² 的图象向右平移1个单位就得到函数 y ＝ x ² －2 x +1的图象．

5、D　

点拨： 抛物线 y ＝ ax ² ，| a |越小，抛物线的开口越大．

6、D　

点拨： y ＝ x ² －4 x +3＝ ( x ² －8 x )+3＝ ( x －4) ² －5．

7、D　

点拨： 抛物线左右平移横坐标变化，而纵坐标不变，平移规律是“左加右减”．

8、B　

点拨： 平移坐标轴相当于把图象反向平移．

9、D　

点拨： 一次函数 y ＝－ x +1中， b ＝1＞0，交于 y 轴的正半轴，排除A、B；二次函数 的顶点坐标是(1，0)，由此可作出判断．

10、C　

点拨： y ＝ ax ² + bx + c 配方为 ，∵ b ² ＝ ac ，

∴ ．当 x ＝0时， y ＝ c ，即 c ＝－4．

∴ ．∵ c ＜0， b ² ≥0，∴ a ＜0．∴ y 有最大值是－3．

二、填空题

11、－90

点拨： 将 y ＝2 x ² －12 x －12进行配方，得 y ＝2( x －3) ² －30，所以 m ＝3， n ＝－30，所以 m n ＝－90.

12、－1

点拨： 当 x ＝－ ＝－ ＝－1时，二次函数 y ＝ x ² +2 x －2有最小值．

13、4

点拨： 由于－ ＝1，解得 b ＝4.

14、＞

15、 解析： 一般情况下，若知道抛物线上的三点坐标，可设二次函数的一般式为y=ax ² +bx+c；若知道顶点坐标（h，k）或对称轴x=h，可设顶点式y=a(x-h) ² +k;若知道抛物线与x轴的两个交点坐标，可设两点式y=a(x-x ₁ )(x-x ₂ )，这样将比较简便.

答案： y=ax ² +bx+c  y=a(x-h) ² +k  y=a(x-x ₁ )(x-x ₂ )

16、 解析： 两个抛物线形状相同，二次系数相同或互为相反数.这里a=-2，又对称轴为x=2，y有最大值-5，即抛物线y=ax ² +bx+c与y=2x ² -4x-1形状相同，

∴a=±2.

又∵二次函数有最大值，∴a=-2.

∴y=-2(x-2) ² -5=-2(x ² -4x+4)-5=-2x ² +8x-13.故解析式为y=-2(x-2) ² -5.

答案： y=-2(x-2) ² -5

三、解答题

17、（1）   （2）

18、 【答案】A
【解析】解：  观察图像:函数与x轴有两个交点，所以（1） 正确；函数与y轴的交点的纵坐标在0到1之间，所以0＜c＜1，故（2）c>1错误；由函数的对称轴 ，而 ，所以 ，所以（3）2a－b<0正确；当 时，函数y的值为 ，观察图像可知： ，所以（4）a+b+c<0错误。故选A。

19、 【答案】2≤S _△OAB ≤8．
【解析】
试题分析：先根据函数图象上点的坐标特征得出m= ，n= ， =- a+b， =- a+b，于是k= a ² ，再由反比例函数系数k的几何意义可知S _△OAC =S _△OBD ，那么S _△OAB =S _△OAC -S _△OBD +S _梯形ABDC =S _梯形ABDC =2a ² ，根据二次函数的性质即可求解．
试题解析：∵A（a，m）、B（2a，n）在反比例函数y= （k＞0）的图象上，
∴m= ，n= ，
∵A（a，m）、B（2a，n）在一次函数y=- x+b图象上，
∴ =- a+b， =- a+b，
解得：k= a ² ，
∴S _△OAB =S _△OAC -S _△OBD +S _梯形ABDC
=S _梯形ABDC
= （ + ）（2a-a）
= × ×a
= k
= × a ²
=2a ² ．
当1≤a≤2时，S _△OAB =2a ² ，随自变量的增大而增大，此时2≤S _△OAB ≤8．
考点：反比例函数系数k的几何意义．

20、 【答案】（1） 交点坐标为 或 ;（2） 存在，当a=3或a=-1时，有且只有一个交点
【解析】
试题分析：（1）当a=5时，一次函数为y=-x+4
则交点满足：
解得  ，
∴交点坐标为 或
（2）把y=-x+a-1代入反比例函数可得：x（-x+a-1）=1
即-x ² +（a-1）x-1=0
当反比例函数与一次函数有且只有一个交点时，△=（a-1） ² -4=0
解得a=3或a=-1
也即存在实数a，当a=3或a=-1时，有且只有一个交点
考点：反比例函数和一次函数交点